Amberly Roberts

Assignment 12: Maximizing Volume

Here's the problem:

Given a 5 x 8 rectangular sheet of material, how should we cut out square pieces from each corner to create a lidless box with maximum volume?

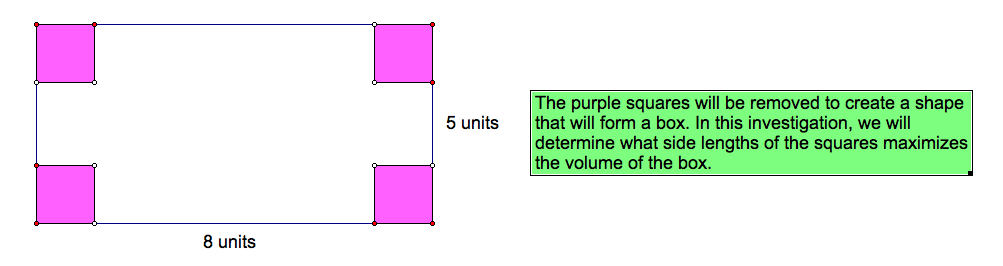
The volume of the box DEPENDS on the length, width, and height of the box. We will create a function in which a variable y (representing volume) will depend on a variable x (representing the length of the squares)

	The spreadsheet indicates that the maximum volume is 18 cubic units. This is achieved when the side lengths of the square are 1 unit in length.   Why does the volume become negative when the side lengths of the square are more than 2.5 units in length? Hint: Think back to the original dimensions of the material.